Automorphic Forms and Number Theory

Date: 11(Wed)-13(Fri), January 2023

Place: Conference Room (110), Graduate School of Science Bldg no. 3, Department of Mathematics, Kyoto University 

Organizers: Atsushi Ichino, Shunsuke Yamana

 

Masataka Chida (Tokyo Denki University)

Sungmun Cho (POSTECH)

Masaaki Furusawa (Osaka Metropolitan University)

Shuji Horinaga (NTT Institute) 

Kaoru Hiraga (Kyoto University) 

Minoru Hirose (Nagoya University)

Ming-Lun Hsieh (National Taiwan University)

Tamotsu Ikeda (Kyoto University)

Hidenori Katsurada (Hokkaido University, Muroran Institute of Technology) 

Takuya Konno (Kyushu University)

Hisayoshi Matsumoto (Tokyo University)

Alberto Minguez (University of Vienna)

Miyu Suzuki (Kyoto University)

Satoshi Wakatsuki (Kanazawa University)

Akihiko Yukie (Kyoto University)

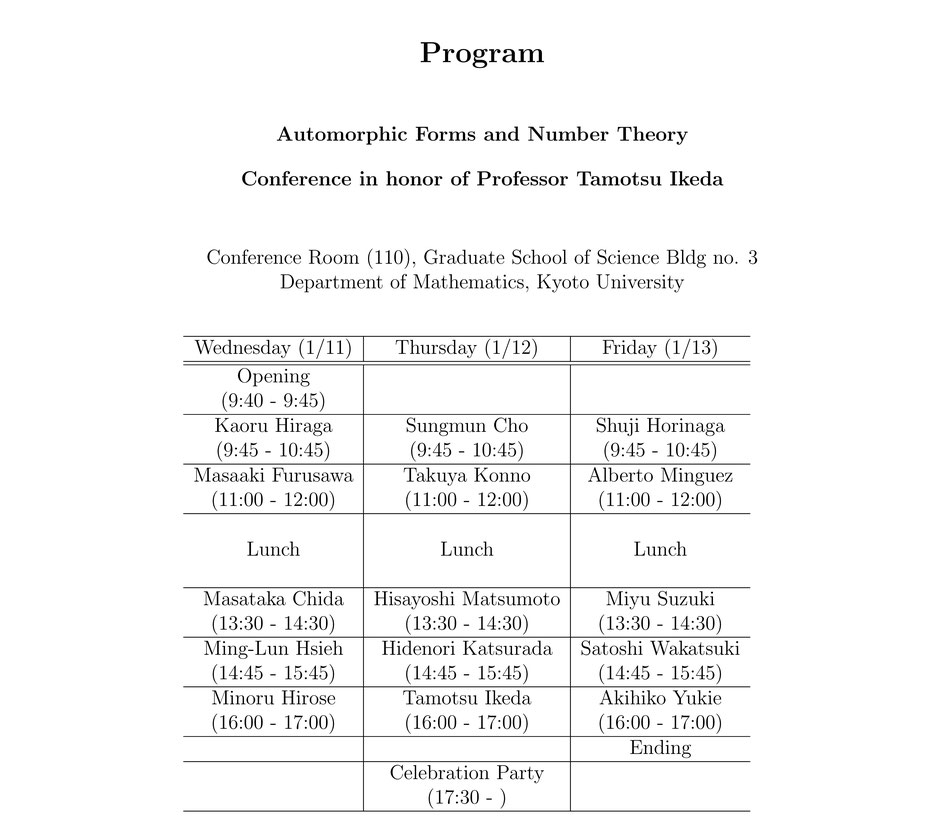
Jan. 11 (Wed.)

9:40 -- 9:45 Opening

9:45 -- 10:45 Kaoru Hiraga (Kyoto University)

Endoscopy for covering groups of anisotropic inner forms of GL(2)

Langlands functoriality for covering groups of quasi-split reductive groups has advanced in recent years. On the other hand, little is known about Langlands functoriality for covering goups of reductive groups that are not quasi-split. In this talk, I will explain the endoscopy for covering groups of even degree of anisotropic inner forms of GL(2). This is a joint work with T.Ikeda.

11:00 -- 12:00 Masaaki Furusawa (Osaka Metropolitan University)

On a certain Ichino-Ikeda type formula and the generalized Böcherer conjecture

(Joint work with Kazuki Morimoto)
We discuss the Ichino-Ikeda type formula for the Bessel periods in the case of (SO(5),SO(2)). As a corollary of our formula, we obtain an explicit formula relating certain weighted averages of Fourier coefficients of holomorphic Siegel cusp forms of degree two which are Hecke eigenforms to central special values of L-functions. The formula is regarded as a natural generalization of Böcherer’s conjecture to the non-trivial toroidal character case.

13:30 -- 14:30 Masataka Chida (Tokyo Denki University)

Arithmetic diagonal cycles on Kuga-Sato varieties

In this talk, we will discuss the construction of algebraic cycles on Kuga-Sato varieties over unitary Shimura varieties. A variant of the arithmetic Gan-Gross-Prasad conjecture was proposed by Rapoport-Smithling-Zhang, which is a conjectural generalization of the Gross-Zagier formula. We will formulate an analogue of the conjecture for higher weight cases.

14:45 -- 15:45 Ming-Lun Hsieh (National Taiwan University)

p-adic L-functions for U(3)xU(2) and the Ichino-Ikeda conjecture

In this talk, I will talk about the p-adic interpolation of Gross-Prasad periods in the setting of U(3)xU(2). Thanks to the Ichino-Ikeda conjecture established by R. Beuzart-Plessis-Y. Liu-W. Zhang-X. Zhu in the stable case and R. Beuzart-Plessis-Chaudouard-Zydor in the endoscopic case, this leads to a construction of the five variable p-adic L-functions associated with Hida families for U(3)xU(2). This is a joint work in progress with M. Harris and S. Yamana.

16:00 -- 17:00 Minoru Hirose (Nagoya University)

Euler sums and cyclotomic associators

 

Euler sums are real numbers defined by iterated integrals on the projective line minus 0,∞,1,-1. In this talk, we introduce a family of linear relations among Euler sums which exhausts all motivic linear relations. This gives an explicit description of the level two motivic Galois group. We also show that the level two motivic Galois group coincides with the cyclotomic Grothendieck-Teichmüller group introduce by Benjamin Enriquez. Some part of this talk is based on a joint work with Nobuo Sato.

Jan. 12 (Thu.)

9:45 -- 10:45 Sungmun Cho (POSTECH)

Orbital integrals for gl_n and smoothening

In this talk, we will introduce a new method of analyzing the orbital integral for a regular semisimple element and for the unit element of the Hecke algebra in gl_n defined over any local field of characteristic 0 or > n, using smoothening of a certain scheme defined over DVR. As an application, we will provide a closed formula for n=2,3 and a lower bound for any n>3. We will also propose a conjecture about estimation of a "potential" formula for gl_n. This is a joint work with Yuchan Lee.

11:00 -- 12:00 Takuya Konno (Kyushu University)

On the Satake isomorphism

We present a representation theoretic proof of the well-known Satake’s isomorphism for unramified Hecke algebra. The key ingredients are an extension of Borel’s description of modules over affine Hecke algebras, and the structure theorem for the Bernstein center.

13:30 -- 14:30 Hisayoshi Matsumoto (Tokyo University)

Gevrey completion of a Whittaker module over sl_2　(joint work with Y. Yamaguchi)

Goodman and Wallach constructed Whittaker vectors in the Gevrey completion of Verma modules. Such vectors can be regarded as differential operators of infinite order from principal series representations to Whittaker models. In this talk, we construct highest weight vectors in the Gevrey completion of a Whittaker module over sl_2. They give the inverse of the Goodman-Wallach operators.

14:45 -- 15:45 Hidenori Katsurada (Hokkaido University, Muroran Institute of Technology)

Congruence between certain lifts and Harder's conjecture

Let $f$ be a primitive form in $S_{2k+j-2}(SL_2(\ZZ))$ with $j$ an even positive integer. Harder's conjecture asserts that the Hecke eigenvalues of $f$ should be related with those of a certain Hecke eigenform in $S_{\det^k \otimes Sym^j}(Sp_2(\ZZ))$ modulo some prime ideal. One of main difficulties in treating this conjecture arises from the fact that it is not concerned with the congruence between Hecke eigenvalues of two Hecke eigenforms. In this talk, we propose several conjectures on the congruence between the Klinegen-Eisenstein lift of the Duke-Imamoglu-Ikeda lift or of the Miyawaki lift and a certain lift of a Hecke eigenform in $S_{\det^k \otimes Sym^j}(Sp_2(\ZZ))$. These conjectures imply Harder's conjecture. In particular, we prove our conjecture, and therefore Harder's in the case that $k$ is even and $j \equiv 0 \text{ mod } 4$. We also talk about our ongoing project for other cases. Some part of this talk is based on a joint work with H. Atobe, M. Chida, T. Ibukiyama and T. Yamauchi.

16:00 -- 17:00 Tamotsu Ikeda (Kyoto University)

On the theory of the liftings

This is an expository talk on the theory of the liftings. I will explain the theory of the Duke-Imamoglu-Ibukiyama lifting and the Miyawaki lifting and related topics. I will also explain how these lifting can be understood in terms of the Arthur endoscopic classification.

17:30 -- Celebration Party

 

Jan. 13 (Fri.)

9:45 -- 10:45 Shuji Horinaga (NTT Instutute)

Cuspidal components of Siegel modular forms for large discrete series representations of $\mathrm{Sp}_4(\mathbb{R})$

As far as I know, there are no known results of an explicit description of cuspidal components for non-holomorphic automorphic forms except for nearly holomorphic modular forms. In this talk, we investigate the cuspidal components and the structures for automorphic forms on $\mathrm{Sp}_4$ which generate large discrete series representations by the explicit formulas of degenerate Whittaker functions of large discrete series representations. This talk is based on the joint work with Hiro-aki Narita.

11:00 -- 12:00 Alberto Minguez (University of Vienna)

Local Transfer for quasi-split classical groups and congruences mod \ell

Let \pi and \pi’ be two \ell-adic irreducible cuspidal representations of a quasi-split classical group G and let \sigma and \sigma’ be their respective Langlands’s transfers to GL(N). Assume \pi and \pi’ are integral and denote r_\ell(\pi) and r_\ell(\pi') their reduction modulo \ell. We will show that, if r_\ell(\pi) \leq r_\ell(\pi’), then r_\ell(\sigma) and r_\ell(\sigma’) have a unique generic irreducible component in common. This is joint work with Vincent Sécherre.

13:30 -- 14:30 Miyu Suzuki (Kyoto University)

Towards the full epsilon dichotomy for linear periods

Let G be an inner form of GL(n) over a local field F and H be its symmetric subgroup which is an inner form of GL(m) over a quadratic extension of F. An H-invariant linear form on a representation of G is called a linear period. Prasad and Takloo-Bighash formulated a conjecture about necessary conditions for representations of G to be distinguished. In this talk, I will reformulate their conjecture so that it characterizes distinguished representations in generic L-packets in terms of epsilon factors and the characters of the S-groups. I will also explain that this reformulated epsilon dichotomy follows from the conjectural multiplicity formula, which is proposed by Chen Wan for general spherical varieties.

14:45 -- 15:45 Satoshi Wakatsuki (Kanazawa University)

Twisted limit multiplicity formulas for GL(n)

In this talk, I will discuss our ongoing research on twisted limit multiplicity formulas for GL(n). First, I give a summary on (non-twisted) limit multiplicity formulas, which have been already proved for a wide class of reductive groups. Next, I introduce twisted limit multiplicity formulas for GL(n) with respect to symplectic, orthogonal, and unitary involutions, and present a conjecture on the measures of limits of multiplicities for the unitary involution. This conjecture is based on some results in the paper of Hiraga-Ichino-Ikeda on the formal degree conjecture. This is a joint work with Miyu Suzuki and Yugo Takanashi.

16:00 -- 17:00 Akihiko Yukie (Kyoto University)

On density theorems and rational orbits related to prehomogeneous vector spaces

After reviewing the interpretation of rational orbits of generic points, we discuss recent density theorems related to prehomogenous vector spaces. Then we explain examples of the GIT stratification which describes rational orbits of points where the action is bad.

17:00 -- 17:05 Ending